This page contains SVM and Kernel-related programs implemented in MatLab or C.
ROBUST KERNEL-BASED REGRESSION USING ORTHOGONAL MATCHING PURSUIT
Kernel methods are widely used for approximation of nonlinear functions in classic regression problems, using standard techniques, e.g., Least Squares, for denoising data samples in the presence of white Gaussian noise. However, the approximation deviates greatly, when impulse noise outlying the data enters the scene. We present a robust kernel-based method, which exploits greedy selection techniques, particularly Orthogonal Matching Pursuit (OMP), in order to recover the sparse support of the outlying vector; at the same time, it approximates the non-linear function via the mapping to a Reproducing Kernel Hilbert Space (RKHS).
- Manuscript in pdf format.
- Code. (implemented in Matlab).
Complex Support Vector Machines for Regression and Quaternary Classification
We present a support vector machines (SVM) rationale suitable for regression and quaternary classification problems that use complex data, exploiting the notions of widely linear estimation and pure complex kernels. The recently developed Wirtinger’s calculus on complex RKHS is employed in order to compute the Lagrangian and derive the dual optimization problem. We prove that this approach is equivalent with solving two real SVM tasks exploiting a specific real kernel, which is induced by the chosen complex kernel.
- Manuscript in pdf format.
- Code. (implemented in Matlab). Open the file readme.txt for details.
Online Learning with Kernels
As Kernel-based adaptive learning (or Kernel Adaptive Filtering) is growing in popularity we decided to write a small introductory text explaining the most widely used algorithms of this class, namely the Kernel Least Mean Squares (Kernel LMS) and the kernel recursive least squares (Kernel RLS) algorithms. In this page you will also find extensive simulations comparing these algorithms in standard non-linear signal processing tasks, as well as the respective Matlab/C code to run these algorithms yourself. The material will be updated frequently.
Online Learning in Reproducing Kernel Hilbert Spaces - Introductory text
- Chapter 1: Reproducing Kernel Hilbert Spaces. This chapter contains an introduction to the theory of Reproducing Kernel Hilbert Spaces (RKHS). Most known mathematical results are stated here. Although we compiled this chapter as an introductory text for engineers, which are interested mainly in the most important results, we have, also, included several proofs of results that are of particular interest to the machine learning community. Such theorems include the celebrated representer theorem, theorems that involve the definition of RKHS, important properties, the fact that the popular Gaussian RBF function is indeed a kernel, e.t.c. These can be omitted by those who are not interested in delving into the theory of RKHS.
- Chapter 2: Least Squares Algorithms. Recently, kernel-based generalizations of the popular Least Mean Squares (LMS) and Recursive Least Squares (RLS) algorithms have been proposed, the so called Kernel LMS (KLMS), Kernel APSM (KAPSM) and Kernel RLS (KRLS), as a means to treat non-linear adaptive signal processing tasks. This chapter contains the theoretical derivations of these algorithms in RKHS, pseudocodes, and several simulation results. The Matlab code for the algorithms and the simulations can be found below.
- Manuscript in pdf format.
- Code. (implemented in Matlab and C).
The archive includes code for the following algorithms: a) Kernel Least Mean Square (KLMS), b) Quantized KLMS (QKLMS), c) Quantized Kernel Adaptive Projected Subgradient Method (QKAPSM) and d) Kernel RLS (KRLS). Remember to execute the command "mex fast_real_output_kernel_computation.c", before running the simulations, to produce the necessary mex binaries. - Geogebra Interactive files.
Gaussian Kernel,
Laplacian Kernel
Polynomial (Homogeneous)
Polynomial (Inhomogeneous)
The Augmented Complex Kernel LMS
Recently, a unified framework for adaptive kernel based signal processing of complex data was presented by the authors, which, besides offering techniques to map the input data to complex Reproducing Kernel Hilbert Spaces, developed a suitable Wirtinger-like Calculus for general Hilbert Spaces. In this short paper, the extended Wirtinger's calculus is adopted to derive complex kernel-based widely-linear estimation filters. Furthermore, we illuminate several important characteristics of the widely linear filters. We show that, although in many cases the gains from adopting widely linear estimation filters, as alternatives to ordinary linear ones, are rudimentary, for the case of kernel based widely linear filters significant performance improvements can be obtained.
Below you can find the preprint version of the corresponding paper, as well as the (MatLab and C) code used in the experiments.
Adaptive Learning in Complex Reproducing Kernel Hilbert Spaces employing Wirtinger's subgradients
This paper presents a wide framework for nonlinear online learning tasks in the context of complex signal processing. The (complex) input data are mapped into a complex Reproducing Kernel Hilbert Space (RKHS), where the learning phase is taking place. Both pure complex kernels and real kernels (via the complexification trick) can be employed. Moreover, any convex, continuous and not necessarily differentiable function can be used to measure the loss between the output of the specific system and the desired response. The only requirement is the subgradient of the adopted loss function to be available in an analytic form. In order to derive analytically the subgradients, the principles of the (recently developed) Wirtinger’s Calculus in complex RKHS are exploited. Furthermore, both linear and widely linear (in RKHS) estimation filters are considered. To cope with the problem of increasing memory requirements, which is present in almost all online schemes in RKHS, the projection onto classed balls sparsification strategy is adopted. We demonstrate the effectiveness of the proposed framework in a non linear channel identification problem, a non linear channel equalization problem and a QPSK equalization scheme, using both circular and non circular sources.
Below you can find the preprint version of the corresponding paper, as well as the (MatLab and C) code used in the experiments. This includes the NCKLMS1 and NCKLMS2, the ANCKLMS, the complexified CKAPSM and the pure Complex KAPSM.
Extension of Wirtinger Calculus in RKH spaces and the Complex Kernel LMS.
Over the last decade, kernel methods for nonlinear processing have successfully been used in the machine learning community. The primary mathematical tool employed in these methods is the notion of the Reproducing Kernel Hilbert Space. However, so far, the emphasis has been on batch techniques. It is only recently, that online techniques have been considered in the context of adaptive signal processing tasks and for the case of real valued sequences. To the best of our knowledge, no kernel-based strategy has been developed, so far, that is able to deal with complex valued signals. Moreover, although the real reproducing kernels are used in an increasing number of machine learning problems, complex kernels have not, yet, been used, in spite of their potential interest in applications that deal with complex signals, with Communications being a typical example. In this paper, we present a general framework to attack the problem of adaptive filtering of complex signals, using either real reproducing kernels, taking advantage of a technique called \textit{complexification} of real RKHSs, or complex reproducing kernels, highlighting the use of the complex gaussian kernel. In order to derive gradients of operators that need to be defined on the associated complex RKHSs, we employ the powerful tool of Wirtinger's Calculus, which has recently attracted much attention in the signal processing community. Writinger's calculus simplifies computations and offers an elegant tool for treating complex signals. To this end, in this paper, the notion of Writinger's calculus is extended, for the first time, to include complex RKHSs and use it to derive several realizations of the Complex Kernel Least-Mean-Square (CKLMS) algorithm. Experiments verify that the CKLMS offers significant performance improvements over the traditional complex LMS or Widely Linear complex LMS (WL-LMS) algorithms, when dealing with nonlinearities.
- paper (preprint)
- Wirtinger's Calculus in RKHS (report)
- code (implemented in Matlab)
- Instructions (readme)
Adaptive kernel based image denoising employing semiparametric regularization.
We have developed a novel approach, based on the theory of Reproducing Kernel Hilbert Spaces (RKHS), for the problem of Noise Removal in the spatial domain. The proposed methodology has the advantage that it is able to remove any kind of additive noise (impulse, gaussian, uniform e.t.c.) from any digital image, in contrast to the most common denoising technics that are noise-dependent. The problem is cast as an optimization task in a RKHS, by taking advantage of the celebrated Representer Theorem in its semi-parametric formulation. The semi-parametric formulation, although known in theory, has so far found limited, to our knowledge, application. However, in the image denoising problem its use is dictated by the nature of the problem itself. The need for edge preservation naturally leads to such a modeling. Examples verify that in the presence of gaussian noise the proposed methodology performs well compared to wavelet based techniques and outperforms them significantly in the presence of impulse or mixed noise. For more information you have to read the paper. See below a list of downloads
- paper (preprint)
- code (implemented in C)
- Windows Executable
- Test examples (excel file with input parameters-results and images rar file)
- Instructions (readme)
Examples:
Fig. 1
- (a) The lena image obtained from the Waterloo Image Repository.
- (b) The lena image corrupted by 30% of additive impulse noise (the impulses are uniformly distributed in [-128, 128]) (PSNR=16.60 dB).
- (c) The denoised image according to the proposed methodology (PSNR=33.20 dB).
 (a)
(a)
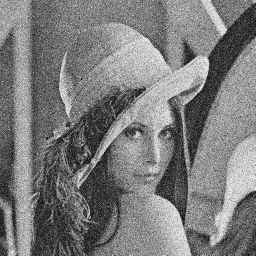 (b)
(b)
 (c)
(c)
Fig. 2
- (a) The lena image obtained from the Waterloo Image Repository.
- (b) The lena image corrupted by 50% of additive impulse noise (the impulses are uniformly distributed in [-128, 128]) (PSNR=14.41 dB).
- (c) The denoised image according to the proposed methodology (PSNR=30.71 dB).
 (a)
(a)
 (b)
(b)
 (c)
(c)
Fig. 3
- (a) The lena image obtained from the Waterloo Image Repository.
- (b) The lena image corrupted by additive gaussian noise (sigma=20) (PSNR=22.14 dB).
- (c) The denoised image according to the proposed methodology (PSNR=31.12 dB).
 (a)
(a)
 (b)
(b)
 (c)
(c)
Fig. 4
- (a) The lena image obtained from the Waterloo Image Repository.
- (b) The lena image corrupted by 20% of additive impulse noise (the impulses are uniformly distributed in [-128, 128]) and additive gaussian noise (sigma=10) (PSNR=17.98 dB).
- (c) The denoised image according to the proposed methodology (PSNR=32.27 dB).
 (a)
(a)
 (b)
(b)
 (c)
(c)